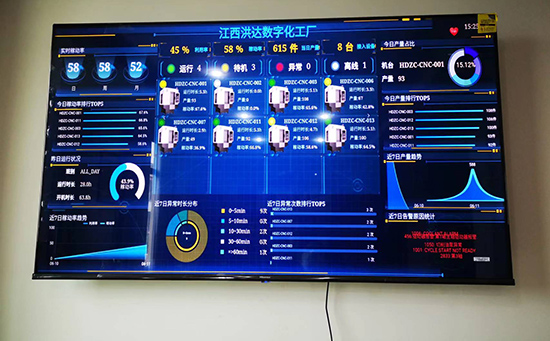
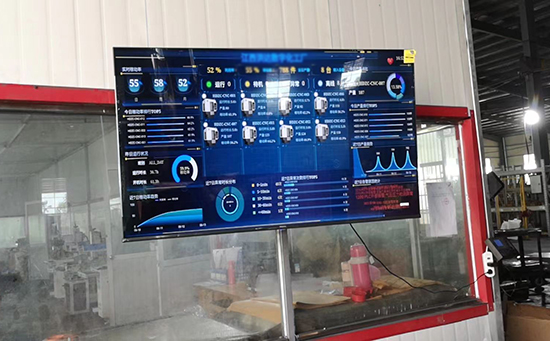
ERP系统 & MES 生产管理系统
10万用户实施案例,ERP 系统实现微信、销售、库存、生产、财务、人资、办公等一体化管理
Excel中的几何平均数:全面详解及计算方法
Excel作为广泛使用的电子表格软件,不仅可以进行基本的数据分析和计算,还提供了丰富的函数来支持各种数学运算。其中,几何平均数作为重要的统计量之一,在诸多应用中占据着重要位置。本文将详细介绍Excel中几何平均数的概念、计算方法及其实际应用,帮助您全面了解和运用这一统计工具。
什么是几何平均数?
几何平均数是一组数据的乘积的N次根,其中N为数据的个数。与算术平均数不同,几何平均数更多地用于计算比率和增长率,尤其在涉及多期数据的复合增长时特别有用。
Excel中的几何平均数函数
Excel提供了GEOMEAN函数来计算一组数据的几何平均数。使用该函数可以轻松地对数据进行几何平均数的计算,而无需手动编写复杂的公式。
示例:
“`excel
=GEOMEAN(A1:A10)
“`
这个公式将计算A1到A10单元格范围内数据的几何平均数。
如何计算几何平均数?
几何平均数的计算步骤相对简单:
1. 将所有数据相乘得到总乘积。
2. 将总乘积的N次方根,其中N为数据的个数。
Excel的GEOMEAN函数实现了这些步骤,并能够处理各种数据类型,包括小数和负数。
几何平均数的应用场景
几何平均数广泛应用于金融、经济学、生物学等领域,特别适用于以下情况:
– 计算投资组合的年化收益率。
– 测算生产率和增长率的变化。
– 分析多期数据的复合增长。
Excel几何平均数的局限性
尽管Excel的几何平均数函数非常便利,但在应用过程中也存在一些局限性:
– 对于包含零值或负值的数据,几何平均数的计算结果可能无意义或不适用。
– 几何平均数对异常值(如极端大或小的数据点)比较敏感,需要谨慎处理。
结合实例进行深入理解
为了帮助读者更好地理解Excel中几何平均数的实际应用,我们提供一个简单的实例:
假设有一家公司的销售额如下(单位:万元):10, 12, 15, 18, 20。使用Excel的GEOMEAN函数可以计算出这些销售额的几何平均数,从而评估公司销售额的年均增长率。
结语
通过本文的详细介绍,您不仅了解了Excel中几何平均数的计算方法和应用场景,还掌握了如何利用Excel的函数来进行几何平均数的快速计算。在实际工作和研究中,熟练运用几何平均数将为您的数据分析和决策提供强有力的支持。
希望本文能够帮助您更好地利用Excel进行数据分析,提升工作效率和决策准确性。