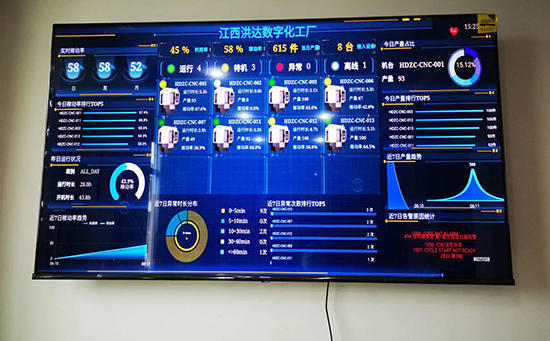
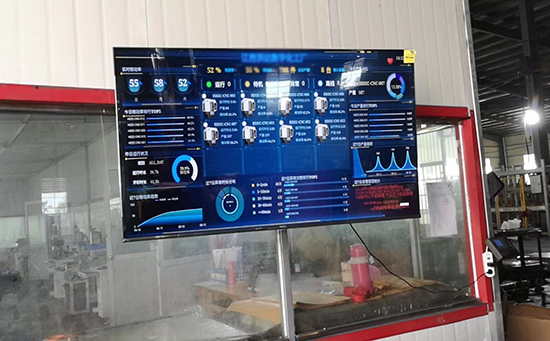
ERP系统 & MES 生产管理系统
10万用户实施案例,ERP 系统实现微信、销售、库存、生产、财务、人资、办公等一体化管理
Understanding and Calculating Average Values: A Comprehensive Guide
Average values play a fundamental role in statistical analysis across various disciplines, providing insights into central tendencies within data sets. Whether you’re a student learning basic arithmetic or a professional analyzing complex datasets, understanding how to calculate and interpret averages is crucial. This article delves into the concept of averages, different types of averages, methods of calculation, and practical applications.
What is an Average?
An average, in simplest terms, is a measure that represents a central value of a set of numbers. It provides a typical value around which the data tends to cluster. Understanding averages helps in summarizing data efficiently, making comparisons, and drawing conclusions.
Types of Averages
There are several types of averages commonly used:
– Arithmetic Mean: The arithmetic mean is the sum of all values in a dataset divided by the number of values. It’s the most widely used average.
– Median: The median is the middle value in a sorted, ascending or descending, list of numbers.
– Mode: The mode is the value that appears most frequently in a dataset.
– Weighted Average: Weighted averages assign different weights to different values based on their importance or frequency.
Calculating Averages
Arithmetic Mean Calculation
The arithmetic mean \( \bar{x} \) of a dataset with \( n \) values \( x_1, x_2, \ldots, x_n \) is calculated as:
\[ \bar{x} = \frac{x_1 + x_2 + \ldots + x_n}{n} \]
Median Calculation
To find the median of a dataset:
1. Arrange the values in ascending order.
2. If \( n \) (number of values) is odd, the median is the middle value.
3. If \( n \) is even, the median is the average of the two middle values.
Mode Calculation
The mode is determined by identifying the value that appears most frequently in the dataset.
Applications of Averages
Averages are used extensively in various fields:
– Education: Teachers use averages to assess student performance.
– Finance: Financial analysts use averages to study market trends.
– Healthcare: Averages help in understanding patient data and treatment effectiveness.
– Sports: Average statistics help evaluate player performance.
– Research: Scientists use averages to analyze experimental results.
Challenges and Considerations
While averages provide valuable insights, they can sometimes oversimplify complex data:
– Outliers: Extreme values can skew averages.
– Data Distribution: Averages may not accurately represent skewed or non-normal distributions.
– Context: Averages should always be interpreted in the context of the data and its specific characteristics.
Conclusion
A thorough understanding of averages is essential for anyone dealing with data analysis. By grasping the nuances of different average types, methods of calculation, and their applications, you gain a powerful tool for interpreting and summarizing data effectively. Whether you’re analyzing financial reports, conducting scientific research, or simply managing personal finances, knowing how to calculate and interpret averages equips you with invaluable analytical skills. Embrace the versatility of averages in making informed decisions across diverse fields.